问题描述
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
例如,给定如下二叉树: root = [3,5,1,6,2,0,8,null,null,7,4]
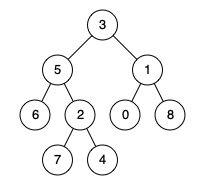
示例 1:
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出: 3
解释: 节点 5 和节点 1 的最近公共祖先是节点 3。
示例 2:
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出: 5
解释: 节点 5 和节点 4 的最近公共祖先是节点 5。因为根据定义最近公共祖先节点可以为节点本身。
说明:
- 所有节点的值都是唯一的。
- p、q 为不同节点且均存在于给定的二叉树中。
注意:本题与主站 236 题相同:https://leetcode-cn.com/problems/lowest-common-ancestor-of-a-binary-tree/
解题思路
关键在于找到结点的祖先结点。
可以在递归的过程中使用一个字典记录每个结点的父结点。
然后再对结点 \(p\) 所有的祖先结点进行标记。
最后遍历结点 \(q\) 的祖先结点的过程中,如果某个已经被标记过,说明该结点即为 \(p\) 和 \(q\) 的最近公共祖先结点。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47 | class Solution:
def lowestCommonAncestor(
self, root: "TreeNode", p: "TreeNode", q: "TreeNode"
) -> "TreeNode":
if root is None:
return None
parent = {root.val: ""}
def f(root: "TreeNode") -> None:
if root is None:
return
# 遍历到其中某个结点时,其子结点就可以不用遍历了
if root is p or root is q:
return
# 如果两个结点都已经遍历到了就结束
if p.val not in parent or q.val not in parent:
if root.left:
parent[root.left.val] = root
f(root.left)
if root.right:
parent[root.right.val] = root
f(root.right)
f(root)
# 表示 q 是 p 的祖先结点
if p.val not in parent:
return q
# 表示 p 是 q 的祖先结点
if q.val not in parent:
return p
v = set()
while p.val != root.val:
v.add(p.val)
p = parent[p.val]
while q.val != root.val:
if q.val in v:
break
q = parent[q.val]
return q
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21 | class Solution:
def lowestCommonAncestor(
self, root: "TreeNode", p: "TreeNode", q: "TreeNode"
) -> "TreeNode":
if root is None:
return None
# 遍历到其中某个结点时,其子结点就可以不用遍历了
if root is p or root is q:
return root
l = self.lowestCommonAncestor(root.left, p, q)
r = self.lowestCommonAncestor(root.right, p, q)
# 说明 root 结点是回溯过程中第一个在左右子树中同时存在 p q 结点的
if l and r:
return root
# 最后返回的结果要么是 root,表示 p 和 q 都是 root 的子结点
# 要么是 p 或 q,表示 q 或 p 是它的子结点
return l or r
|
