1765. 地图中的最高点 #

问题描述#

给你一个大小为 m x n 的整数矩阵 isWater ，它代表了一个由陆地和水域单元格组成的地图。

如果 isWater[i][j] == 0 ，格子 (i, j) 是一个陆地格子。

如果 isWater[i][j] == 1 ，格子 (i, j) 是一个水域格子。

你需要按照如下规则给每个单元格安排高度：

每个格子的高度都必须是非负的。

如果一个格子是是水域，那么它的高度必须为 0 。

任意相邻的格子高度差至多为 1 。当两个格子在正东、南、西、北方向上相互紧挨着，就称它们为相邻的格子。（也就是说它们有一条公共边）

找到一种安排高度的方案，使得矩阵中的最高高度值最大。

请你返回一个大小为 m x n 的整数矩阵 height ，其中 height[i][j] 是格子 (i, j) 的高度。如果有多种解法，请返回 任意一个 。

示例 1：
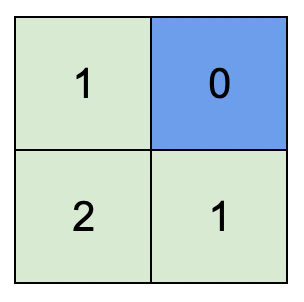
输入：isWater = [[0,1],[0,0]]
输出：[[1,0],[2,1]]
解释：上图展示了给各个格子安排的高度。
蓝色格子是水域格，绿色格子是陆地格。
示例 2：
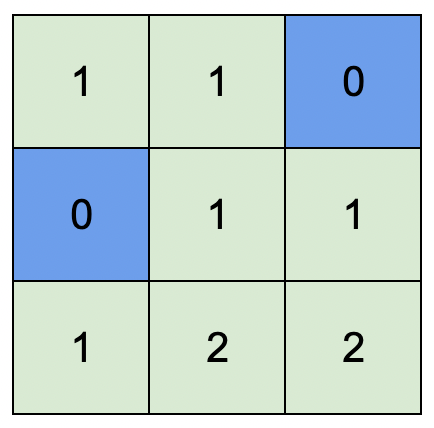
输入：isWater = [[0,0,1],[1,0,0],[0,0,0]]
输出：[[1,1,0],[0,1,1],[1,2,2]]
解释：所有安排方案中，最高可行高度为 2 。
任意安排方案中，只要最高高度为 2 且符合上述规则的，都为可行方案。
提示：

m == isWater.length

n == isWater[i].length

1 <= m, n <= 1000

isWater[i][j] 要么是 0 ，要么是 1 。

至少有 1 个水域格子。

解题思路#

从 isWater[i][j] = 1 的点开始进行广搜。

Python

class Solution:
    def highestPeak(self, g: List[List[int]]) -> List[List[int]]:
        m, n = len(g), len(g[0])
        ans = [[-1] * n for _ in range(m)]
        q = []

        for i in range(m):
            for j in range(n):
                if g[i][j] == 1:
                    q.append(i * n + j)
                    ans[i][j] = 0

        dx, dy = [0, -1, 0, 1], [-1, 0, 1, 0]
        h = 1

        while q:
            qu = []

            while q:
                x = q.pop()
                i, j = divmod(x, n)
                for k in range(4):
                    r, c = i + dx[k], j + dy[k]
                    if 0 <= r < m and 0 <= c < n and ans[r][c] == -1:
                        ans[r][c] = h
                        qu.append(r * n + c)

            h += 1
            q = qu

        return ans

C++

class Solution {
public:
    vector<vector<int>> highestPeak(vector<vector<int>>& g) {
        int m = g.size(), n = g[0].size();
        vector<vector<int>> ans(m, vector<int>(n, -1));
        queue<int> q;

        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (g[i][j] == 1) {
                    q.emplace(i * n + j);
                    ans[i][j] = 0;
                }
            }
        }

        int dx[] = {0, -1, 0, 1}, dy[] = {-1, 0, 1, 0};
        int h = 1;

        while (!q.empty()) {
            int sz = q.size();
            while (sz--) {
                int x = q.front(); q.pop();
                int i = x / n, j = x % n;
                for (int k = 0; k < 4; ++k) {
                    int r = i + dx[k], c = j + dy[k];
                    if (0 <= r && r < m && 0 <= c && c < n && ans[r][c] == -1) {
                        ans[r][c] = h;
                        q.emplace(r * n + c);
                    }
                }
            }
            ++h;
        }

        return ans;
    }
};

时间复杂度：\(\mathcal{O}(mn)\)
空间复杂度：\(\mathcal{O}(mn)\)

1765. 地图中的最高点#

问题描述#

解题思路#

1765. 地图中的最高点 #