1530. 好叶子节点对的数量 #

问题描述#

给你二叉树的根节点 root 和一个整数 distance 。

如果二叉树中两个叶节点之间的 最短路径长度 小于或者等于 distance ，那它们就可以构成一组 好叶子节点对 。

返回树中 好叶子节点对的数量 。

示例 1：
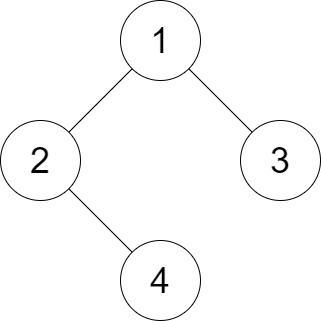
输入：root = [1,2,3,null,4], distance = 3
输出：1
解释：树的叶节点是 3 和 4 ，它们之间的最短路径的长度是 3 。这是唯一的好叶子节点对。
示例 2：
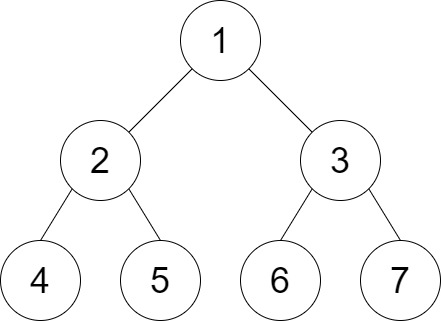
输入：root = [1,2,3,4,5,6,7], distance = 3
输出：2
解释：好叶子节点对为 [4,5] 和 [6,7] ，最短路径长度都是 2 。但是叶子节点对 [4,6] 不满足要求，因为它们之间的最短路径长度为 4 。
示例 3：
输入：root = [7,1,4,6,null,5,3,null,null,null,null,null,2], distance = 3
输出：1
解释：唯一的好叶子节点对是 [2,5] 。
示例 4：
输入：root = [100], distance = 1
输出：0
示例 5：
输入：root = [1,1,1], distance = 2
输出：1
提示：

tree 的节点数在 [1, 2^10] 范围内。

每个节点的值都在 [1, 100] 之间。

1 <= distance <= 10

解题思路#

两个叶子结点之间的距离，为两者离最近的公共祖先结点的距离之和。

所以对个每个结点，分别计算其左右子树中的叶结点与该结点的距离，然后计算满足条件的结点即可。

class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right


class Solution:
    def countPairs(self, root: TreeNode, distance: int) -> int:
        ans = 0

        def f(root: TreeNode) -> dict:
            nonlocal ans
            if root is None:
                return {}

            if root.left is None and root.right is None:
                return {1: 1}  # 距离: 数量

            left = f(root.left)
            right = f(root.right)

            for dl in left:
                for dr in right:
                    if dl + dr <= distance:
                        ans += left[dl] * right[dr]

            # 返回到上一结点时需要加上该结点本身
            # 所以其左右子树中的结点的距离都增加 1
            s = {}
            for d in left:
                if d + 1 < distance:
                    s[d + 1] = left[d]  # 距离加 1
            for d in right:
                if d + 1 < distance:
                    # 该结点在左子树中可能出现过
                    s[d + 1] = s.get(d + 1, 0) + right[d]  # 距离加 1

            return s

        f(root)
        return ans

1530. 好叶子节点对的数量#

问题描述#

解题思路#

1530. 好叶子节点对的数量 #