问题描述
在由 1 x 1 方格组成的 N x N 网格 grid 中,每个 1 x 1 方块由 /、\ 或空格构成。这些字符会将方块划分为一些共边的区域。
(请注意,反斜杠字符是转义的,因此 \ 用 "\\" 表示。)。
返回区域的数目。
示例 1:
输入:
[
" /",
"/ "
]
输出:2
解释:2x2 网格如下:
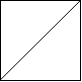
示例 2:
输入:
[
" /",
" "
]
输出:1
解释:2x2 网格如下:
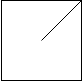
示例 3:
输入:
[
"\\/",
"/\\"
]
输出:4
解释:(回想一下,因为 \ 字符是转义的,所以 "\\/" 表示 \/,而 "/\\" 表示 /\。)
2x2 网格如下:
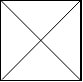
示例 4:
输入:
[
"/\\",
"\\/"
]
输出:5
解释:(回想一下,因为 \ 字符是转义的,所以 "/\\" 表示 /\,而 "\\/" 表示 \/。)
2x2 网格如下:
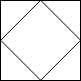
示例 5:
输入:
[
"//",
"/ "
]
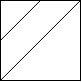
输出:3
解释:2x2 网格如下:
提示:
1 <= grid.length == grid[0].length <= 30grid[i][j] 是 '/'、'\'、或 ' '。
解题思路
把每个格子分成左右两部分,然后对每个格子判断它与左边格子以及上边格子(不用四个方向都判断)的连通性即可。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63 | class UnionFind:
def __init__(self):
self.fa = None
self.size = None
def init_set(self, n: int) -> None:
self.fa = list(range(n))
self.size = [1] * n
def find_set(self, x: int) -> int:
if x != self.fa[x]:
self.fa[x] = self.find_set(self.fa[x])
return self.fa[x]
def union_set(self, x: int, y: int) -> bool:
x, y = self.find_set(x), self.find_set(y)
if x == y: return False
if self.size[x] < self.size[y]: x, y = y, x
self.fa[y] = x
self.size[x] += self.size[y]
return True
def is_connected(self, x: int, y: int) -> bool:
return self.find_set(x) == self.find_set(y)
def count(self) -> int:
return sum(1 for i, x in enumerate(self.fa) if i == x)
class Solution:
def regionsBySlashes(self, grid: List[str]) -> int:
n = len(grid)
uf = UnionFind()
uf.init_set(2 * n * n)
def child(i: int, j: int) -> List[int]:
x = i * n + j
return [x << 1, (x << 1) + 1]
for i in range(n):
for j in range(n):
left, right = child(i, j)
if grid[i][j] == ' ': uf.union_set(left, right)
r, c = i, j - 1
if c >= 0:
ll, rr = child(r, c)
uf.union_set(left, rr)
r, c = i - 1, j
if r >= 0:
ll, rr = child(r, c)
if grid[i][j] == '/' or grid[i][j] == ' ':
if grid[r][c] == '/' or grid[r][c] == ' ':
uf.union_set(left, rr)
else:
uf.union_set(left, ll)
else:
if grid[r][c] == '/' or grid[r][c] == ' ':
uf.union_set(right, rr)
else:
uf.union_set(right, ll)
return uf.count()
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71 | class UnionFind {
public:
vector<int> fa, size;
void init_set(int n) {
fa.resize(n), size.resize(n);
for (int i = 0; i < n; ++i) { fa[i] = i, size[i] = 1; }
}
int find_set(int x) { return x == fa[x] ? x : (fa[x] = find_set(fa[x])); }
bool union_set(int x, int y) {
x = find_set(x), y = find_set(y);
if (x == y) return false;
if (size[x] < size[y]) swap(x, y);
fa[y] = x, size[x] += size[y];
return true;
}
bool is_connected(int x, int y) { return find_set(x) == find_set(y); }
int count() {
int n = fa.size(), cnt = 0;
for (int i = 0; i < n; ++i) if (i == fa[i]) ++cnt;
return cnt;
}
};
class Solution {
public:
int regionsBySlashes(vector<string>& grid) {
int n = grid.size();
auto uf = UnionFind();
uf.init_set(2 * n * n);
auto child = [n] (int i, int j) {
int x = i * n + j;
return make_pair(x << 1, (x << 1) + 1);
};
int r, c, ll, rr, left, right;
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
tie(left, right) = child(i, j);
if (grid[i][j] == ' ') uf.union_set(left, right);
r = i, c = j - 1;
if (c >= 0) {
tie(ll, rr) = child(r, c);
uf.union_set(left, rr);
}
r = i - 1, c = j;
if (r >= 0) {
tie(ll, rr) = child(r, c);
if (grid[i][j] == ' ' || grid[i][j] == '/') {
if (grid[r][c] == ' ' || grid[r][c] == '/') uf.union_set(left, rr);
else uf.union_set(left, ll);
} else {
if (grid[r][c] == ' ' || grid[r][c] == '/') uf.union_set(right, rr);
else uf.union_set(right, ll);
}
}
}
}
return uf.count();
}
};
|




