跳转至

240. 搜索二维矩阵 II#

问题描述#

编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性：

  • 每行的元素从左到右升序排列。
  • 每列的元素从上到下升序排列。

 

示例 1：


输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
输出：true

示例 2：


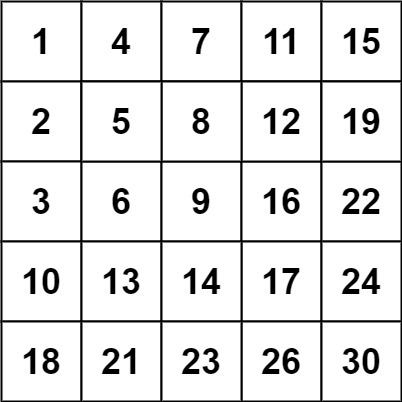
输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20
输出：false

 

提示：

  • m == matrix.length
  • n == matrix[i].length
  • 1 <= n, m <= 300
  • -109 <= matix[i][j] <= 109
  • 每行的所有元素从左到右升序排列
  • 每列的所有元素从上到下升序排列
  • -109 <= target <= 109

解题思路#

从右上角（或左下角）开始搜索，

  • 如果 \(\texttt{target}=\texttt{matrix}[i][j]\)，则直接返回 \(\texttt{true}\)；
  • 如果 \(\texttt{target}\gt\texttt{matrix}[i][j]\)，则说明 \(\texttt{target}\) 存在的话也只能在该位置的右边，\(j=j+1\)；
  • 如果 \(\texttt{target}\lt\texttt{matrix}[i][j]\)，则说明 \(\texttt{target}\) 存在的话也只能在该位置的上边，\(i=i-1\)。
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
class Solution:
    def findNumberIn2DArray(
        self, matrix: List[List[int]], target: int
    ) -> bool:
        if not matrix: return False

        m, n = len(matrix), len(matrix[0])
        i, j = 0, n - 1 # 右上角
        while i < m and j >= 0:
            if matrix[i][j] == target: return True
            elif matrix[i][j] > target: j -= 1
            else: i += 1
        return False

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
class Solution {
public:
    bool findNumberIn2DArray(vector<vector<int>>& matrix, int target) {
        if (matrix.empty()) return false;

        int m = matrix.size(), n = matrix[0].size();
        int i = m - 1, j = 0; // 左下角
        while (i >= 0 && j < n) {
            if (matrix[i][j] == target) return true;
            if (matrix[i][j] > target) --i;
            else ++j;
        }
        return false;
    }
};

时间复杂度：\(\mathcal{O}(m+n)\)
空间复杂度：\(\mathcal{O}(1)\)

返回顶部

在手机上阅读