跳转至

1766. 互质树#

问题描述#

给你一个 n 个节点的树（也就是一个无环连通无向图），节点编号从 0 到 n - 1 ，且恰好有 n - 1 条边，每个节点有一个值。树的 根节点 为 0 号点。

给你一个整数数组 nums 和一个二维数组 edges 来表示这棵树。nums[i] 表示第 i 个点的值，edges[j] = [uj, vj] 表示节点 uj 和节点 vj 在树中有一条边。

当 gcd(x, y) == 1 ，我们称两个数 x 和 y 是 互质的 ，其中 gcd(x, y) 是 x 和 y 的 最大公约数 。

从节点 i 到 根 最短路径上的点都是节点 i 的祖先节点。一个节点 不是 它自己的祖先节点。

请你返回一个大小为 n 的数组 ans ，其中 ans[i]是离节点 i 最近的祖先节点且满足 nums[i] 和 nums[ans[i]] 是 互质的 ，如果不存在这样的祖先节点，ans[i] 为 -1 。

 

示例 1：


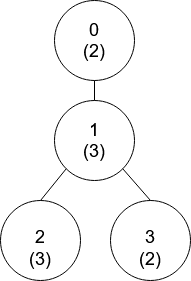
输入：nums = [2,3,3,2], edges = [[0,1],[1,2],[1,3]]
输出：[-1,0,0,1]
解释：上图中，每个节点的值在括号中表示。
- 节点 0 没有互质祖先。
- 节点 1 只有一个祖先节点 0 。它们的值是互质的（gcd(2,3) == 1）。
- 节点 2 有两个祖先节点，分别是节点 1 和节点 0 。节点 1 的值与它的值不是互质的（gcd(3,3) == 3）但节点 0 的值是互质的(gcd(2,3) == 1)，所以节点 0 是最近的符合要求的祖先节点。
- 节点 3 有两个祖先节点，分别是节点 1 和节点 0 。它与节点 1 互质（gcd(3,2) == 1），所以节点 1 是离它最近的符合要求的祖先节点。

示例 2：


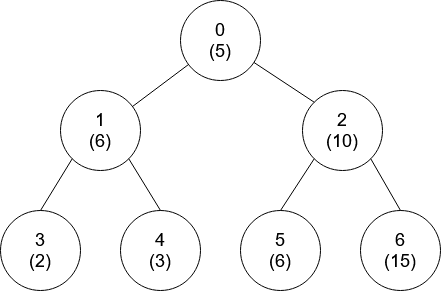
输入：nums = [5,6,10,2,3,6,15], edges = [[0,1],[0,2],[1,3],[1,4],[2,5],[2,6]]
输出：[-1,0,-1,0,0,0,-1]

 

提示：

  • nums.length == n
  • 1 <= nums[i] <= 50
  • 1 <= n <= 105
  • edges.length == n - 1
  • edges[j].length == 2
  • 0 <= uj, vj < n
  • uj != vj

解题思路#

因为每个结点的数值范围为 \([1,50]\)，所以可以预先处理出哪些数是互质的。

1
2
3
4
5
6
7
8
for (int i = 1; i <= 50; ++i) {
    for (int j = i; j <= 50; ++j) {
        if (__gcd(i, j) == 1) {
            g[i].emplace_back(j);
            g[j].emplace_back(i);
        }
    }
}

然后在深度优先遍历树的过程中，将路径中的每个结点按照值将编号保存相同的数组中，并记录每个结点的深度。

所以遍历到某个结点时，可以直接在与它的取值互质的数的数组中寻找结点，因为深度遍历数组中结点添加的顺序也是按照深度排列的，所以只要获取与该结点互质的数的数组中最后一个深度最大结点就是与该结点互质的最近结点。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
static bool f = true;
vector<vector<int>> g;

class Solution {
public:
    Solution() {
        if (f) {
            g.resize(51);
            for (int i = 1; i <= 50; ++i) {
                for (int j = i; j <= 50; ++j) {
                    if (__gcd(i, j) == 1) {
                        g[i].emplace_back(j);
                        g[j].emplace_back(i);
                    }
                }
            }
            f = false;
        }
    }

    vector<int> getCoprimes(vector<int>& nums, vector<vector<int>>& edges) {
        int n = nums.size(), m = edges.size();
        vector<vector<int>> adj(n);

        for (auto &e : edges) {
            adj[e[0]].emplace_back(e[1]);
            adj[e[1]].emplace_back(e[0]);
        }

        vector<int> ans(n, -1);
        vector<vector<int>> path(51);
        vector<int> depth(n, -1);

        function<void(int, int)> dfs = [&] (int u, int d) {
            depth[u] = d;

            int v = -1;
            for (auto x : g[nums[u]]) {
                if (!path[x].empty() && (v == -1 || depth[path[x].back()] > depth[v])) {
                    v = path[x].back();
                }
            }

            if (v != -1) {
                ans[u] = v;
            }

            for (auto x : adj[u]) {
                if (depth[x] == -1) {
                    path[nums[u]].emplace_back(u);
                    dfs(x, d + 1);
                    path[nums[u]].pop_back();
                }
            }
        };

        dfs(0, 0);

        return ans;
    }
};

时间复杂度：\(\mathcal{O}(50n)\)
空间复杂度：\(\mathcal{O}(kn)\)

返回顶部

在手机上阅读